B-树
B-树
当查找的文件较大,且存放在磁盘等直接存取设备中时,为了减少查找过程中对磁盘的读写次数,提高查找效率,基于直接存取设备的读写操作以"页"为单位的特征。
1972年R.Bayer和E.M.McCreight提出了一种称之为B-树的多路平衡查找树。它适合在磁盘等直接存取设备上组织动态的查找表。
B-树的定义
1、B-树的定义
一棵m(m≥3)阶的B-树是满足如下性质的m叉树:
(1)每个结点至少包含下列数据域:
(j,P0,Kl,P1,K2,…,Ki,Pi)
其中:
j为关键字总数
Ki(1≤i≤j)是关键字,关键字序列递增有序:K1 <K2<…<Ki。
Pi(0≤i≤j)是孩子指针。对于叶结点,每个Pi为空指针。
注意:
①实用中为节省空间,叶结点中可省去指针域Pi,但必须在每个结点中增加一个标志域leaf,其值为真时表示叶结点,否则为内部结点。
②在每个内部结点中,假设用keys(Pi)来表示子树Pi中的所有关键字,则有:
keys(P0)<K1<keys(P1)<K2<…<Ki<keys(Pi)
即关键字是分界点,任一关键字Ki左边子树中的所有关键字均小于Ki,右边子树中的所有关键字均大于Ki。
(2)所有叶子是在同一层上,叶子的层数为树的高度h。
(3)每个非根结点中所包含的关键字个数j满足:
。
即每个非根结点至少应有 个关键字,至多有m-1个关键字。
因为每个内部结点的度数正好是关键字总数加1,故每个非根的内部结点至少有
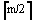
子树,至多有m棵子树。(4)若树非空,则根至少有1个关键字,故若根不是叶子,则它至少有2棵子树。根至多有m-1个关键字,故至多有m棵子树。
2、B-树的结点规模
在大多数系统中,B-树上的算法执行时间主要由读、写磁盘的次数来决定,每次读写尽可能多的信息可提高算法得执行速度。
B-树中的结点的规模一般是一个磁盘页,而结点中所包含的关键字及其孩子的数目取决于磁盘页的大小。
注意:
①对于磁盘上一棵较大的B-树,通常每个结点拥有的孩子数目(即结点的度数)m为50至2000不等
②一棵度为m的B-树称为m阶B-树。
③选取较大的结点度数可降低树的高度,以及减少查找任意关键字所需的磁盘访问次数。
【例】下图给出了一棵高度为3的1001阶B-树。
说明:
①每个结点包含1000个关键字,故在第三层上有100多万个叶结点,这些叶节点可容纳10亿多个关键字。
②图中各结点内的数字表示关键字的数目。
③通常根结点可始终置于主存中,因此在这棵B-树中查找任一关键字至多只需二次访问外存。
3、B-树的存储结构
#define Max l000 //结点中关键字的最大数目:Max=m-1,m是B-树的阶
#define Min 500 //非根结点中关键字的最小数目:Min=┌m/2┐-1
typedef int KeyType; //KeyType应由用户定义
typedef struct node{ //结点定义中省略了指向关键字代表的记录的指针
int keynum; //结点中当前拥有的关键字的个数,keynum《Max
KeyType key[Max+1]; //关键字向量为key[1..keynum],key[0]不用。
struct node *parent; //指向双亲结点
struct node *son[Max+1];//孩子指针向量为son[0..keynum]
}BTreeNode;
typedef BTreeNode *BTree;
注意:
为简单起见,以上说明省略了辅助信息域。在实用中,与每个关键字存储在一起的不是相关的辅助信息域,而是一个指向另一磁盘页的指针。磁盘页中包含有该关键字所代表的记录,而相关的辅助信息正是存储在此记录中。
有的B-树(如第10章介绍的B+树)是将所有辅助信息都存于叶结点中,而内部结点(不妨将根亦看作是内部结点)中只存放关键字和指向孩子结点的指针,无须存储指向辅助信息的指针,这样使内部结点的度数尽可能最大化。
4、5阶B-树示例
【例】下图给出了一棵包含24个英文字母的5阶B-树的存储结构图。
说明:
按照定义,在5阶B-树里,根中的关键字数目可以是1~4,子树数可以是2~5;其它的结点中关键字数目可以是2~4,若该结点不是叶子,则它可以有3~5棵子树。
上一页 下一页
B-树上的基本运算
1、B-树的查找
(1)B-树的查找方法
在B-树中查找给定关键字的方法类似于二叉排序树上的查找。不同的是在每个结点上确定向下查找的路径不一定是二路而是keynum+1路的。
对结点内的存放有序关键字序列的向量key[l..keynum] 用顺序查找或折半查找方法查找。若在某结点内找到待查的关键字K,则返回该结点的地址及K在key[1..keynum]中的位置;否则,确定K在某个key[i]和key[i+1]之间结点后,从磁盘中读son[i]所指的结点继续查找……。直到在某结点中查找成功;或直至找到叶结点且叶结点中的查找仍不成功时,查找过程失败。
【例】下图中左边的虚线表示查找关键字1的过程,它失败于叶结点的H和K之间空指针上;右边的虚线表示查找关键字S的过程,并成功地返回S所在结点的地址和S在key[1..keynum]中的位置2。
(2)B-树的查找算法
BTreeNode *SearchBTree(BTree T,KeyType K,int *pos)
{ //在B-树T中查找关键字K,成功时返回找到的结点的地址及K在其中的位置*pos
//失败则返回NULL,且*pos无定义
int i;
T→key[0]=k; //设哨兵.下面用顺序查找key[1..keynum]
for(i=T->keynum;K<t->key[i];i--); //从后向前找第1个小于等于K的关键字
if(i>0 && T->key[i]==1){ //查找成功,返回T及i
*pos=i;
return T;
} //结点内查找失败,但T->key[i]<K<T->key[i+1],下一个查找的结点应为
//son[i]
if(!T->son[i]) //*T为叶子,在叶子中仍未找到K,则整个查找过程失败
return NULL;
//查找插入关键字的位置,则应令*pos=i,并返回T,见后面的插入操作
DiskRead(T->son[i]); //在磁盘上读人下一查找的树结点到内存中
return SearchBTree(T->Son[i],k,pos); //递归地继续查找于树T->son[i]
}
(3)查找操作的时间开销
B-树上的查找有两个基本步骤:
①在B-树中查找结点,该查找涉及读盘DiskRead操作,属外查找;
②在结点内查找,该查找属内查找。
查找操作的时间为:
①外查找的读盘次数不超过树高h,故其时间是O(h);
②内查找中,每个结点内的关键字数目keynum<m(m是B-树的阶数),故其时间为O(nh)。
注意:
①实际上外查找时间可能远远大于内查找时间。
②B-树作为数据库文件时,打开文件之后就必须将根结点读人内存,而直至文件关闭之前,此根一直驻留在内存中,故查找时可以不计读入根结点的时间。
2、B-树的插入和生成
B-树的生成是从空树起,逐个插入关键字而得到的。
(1)插入关键字K的方法
首先在树中查找K,若找到则直接返回(假设不处理相同关键字的插入);否则查找操作必失败于某个叶子上,然后将K插入该叶子中。若该叶子结点原来是非满(指keynum<Max,即结点中原有的关键字总数小于m-1)的,则插入K后并未破坏B-树的性质,故插入K后即完成了插入操作;若该结点原为满,则K插入后keynum=m,违反B-树性质(3),故须调整使其维持B-树性质不变。
调整操作:
将违反性质(3)的结点以中间位置上的关键字 为划分点,将该
结点(不妨设是*current):
(m,P0,K1,P1,…,Km,Pm) //Ki表示key[i],Pi表示son[i]
"分裂"为两个结点:
并将中间关键字 (和新结点指针new一起插入到*current的双亲*parent中。
注意:
①当m为奇数时,分裂后的两结点中的关键字数目相同,均是半满;
②若m为偶数,则*new中关键字数比*current中关键字数多1。
结点的分裂过程见下图。
其中i表示key和son向量的下标。
注意:
当和新结点的地址一起插入已满的双亲后,双亲也要做分裂操作。最坏情况是,从被插入的叶子到根的路径上各结点均是满结点,此时,插入过程中的分裂操作一直向上传播到根。当根分裂时,因根没有双亲,故需建立一个新的根,此时树长高一层。
(2)B-树的生成
由空树开始,逐个插入关键字,即可生成B-树。
【例】以关键字序列(a,g,f,b,k,d,h,m,i,e, s,i,r,x,c,l,n,t,u,p)建立一棵5阶B-树的生长过程【参见动画演示】
注意:
①当一结点分裂时所产生的两个结点大约是半满的,这就为后续的插入腾出了较多的空间,尤其是当m较大时,往这些半满的空间中插入新的关键字不会很快引起新的分裂。
②向上插人的关键字总是分裂结点的中间位置上的关键字,它未必是正待插入该分裂结点的关键字。因此,无论按何次序插入关键字序列,树都是平衡的。
3、B-树的删除
(1)删除操作的两个步骤
第一步骤:在树中查找被删关键字K所在的地点
第二步骤:进行删去K的操作
(2)删去K的操作
B-树是二叉排序树的推广,中序遍历B-树同样可得到关键字的有序序列(具体遍历算法【参见练习】)。任一关键字K的中序前趋(后继)必是K的左子树(右子树)中最右(左)下的结点中最后(最前)一个关键字。
若被删关键字K所在的结点非树叶,则用K的中序前趋(或后继)K'取代K,然后从叶子中删去K'。从叶子*x开始删去某关键字K的三种情形为:
情形一:若x->keynum>Min,则只需删去K及其右指针(*x是叶子,K的右指针为空)即可使删除操作结束。
注意:
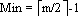
情形二:若x->keynum=Min,该叶子中的关键字个数已是最小值,删K及其右指针后会破坏B-树的性质(3)。若*x的左(或右)邻兄弟结点*y中的关键字数目大于Min,则将*y中的最大(或最小)关键字上移至双亲结点*parent中,而将*parent中相应的关键字下移至x中。显然这种移动使得双亲中关键字数目不变;*y被移出一个关键字,故其keynum减1,因它原大于Min,故减少1个关键字后keynum仍大于等于Min;而*x中已移入一个关键字,故删K后*x中仍有Min个关键字。涉及移动关键字的三个结点均满足B-树的性质(3)。 请读者验证,上述操作后仍满足B-树的性质(1)。移动完成后,删除过程亦结束。
情形三:若*x及其相邻的左右兄弟(也可能只有一个兄弟)中的关键字数目均为最小值Min,则上述的移动操作就不奏效,此时须*x和左或右兄弟合并。不妨设*x有右邻兄弟*y(对左邻兄弟的讨论与此类似),在*x中删去K及其右子树后,将双亲结点*parent中介于*x和*y之间的关键字K,作为中间关键字,与并x和*y中的关键字一起"合并"为一个新的结点取代*x和*y。因为*x和*y原各有Min个关键字,从双亲中移人的K'抵消了从*x中删除的K,故新结点中恰有2Min(即2「m/2」-2≤m-1)个关键字,没有破坏B-树的性质(3)。但由于K'从双亲中移到新结点后,相当于从*parent中删去了K',若parent->keynum原大于Min,则删除操作到此结束;否则,同样要通过移动*parent的左右兄弟中的关键字或将*parent与其 左右兄弟合并的方法来维护B-树性质。最坏情况下,合并操作会向上传播至根,当根中只有一个关键字时,合并操作将会使根结点及其两个孩子合并成一个新的根,从而使整棵树的高度减少一层。
删除5阶B-树的h、r、p、 d等关键字的过程【参见动画演示】。
分析:
第1个被删的关键字h是在叶子中,且该叶子的keynum>Min(5阶B-树的Min=2),故直接删去即可。第2个删去的r不在叶子中,故用中序后继s取代r,即把s复制到r的位置上,然后从叶子中删去s。第3个删去的p所在的叶子中的关键字数目是最小值Min,但其右兄弟的keynum>Min,故可以通过左移,将双亲中的s移到p所在的结点,而将右兄弟中最小(即最左边)的关键字t上移至双亲取代s。当删去d时,d所在的结点及其左右兄弟均无多余的关键字,故需将删去d后的结点与这两个兄弟中的一个(图中是选择左兄弟(ab))及其双亲中分隔这两个被合并结点的关键字c合并在一起形成一个新结点(abce)。但因为双亲中失去c后keynum<Min,故必须对该结点做调整操作,此时它只有一个右兄弟,且右兄弟无多余的关键字,不可能通过移动关键字来解决。因此引起再次合并,因根只有一个关键字,故合并后树高度减少一层,从而得到上图的最后一个图。
B-树的高度及性能分析
B-树上操作的时间通常由存取磁盘的时间和CPU计算时间这两部分构成。B-树上大部分基本操作所需访问盘的次数均取决于树高h。关键字总数相同的情况下B-树的高度越小,磁盘I/O所花的时间越少。
与高速的CPU计算相比,磁盘I/O要慢得多,所以有时忽略CPU的计算时间,只分析算法所需的磁盘访问次数(磁盘访问次数乘以一次读写盘的平均时间(每次读写的时间略有差别)就是磁盘I/O的总时间)。
1、B-树的高度
定理9.1 若n≥1,m≥3,则对任意一棵具有n个关键字的m阶B-树,其树高h至多为:
logt((n+1)/2)+1。
这里t是每个(除根外)内部结点的最小度数,即
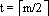
由上述定理可知:B-树的高度为O(logtn)。于是在B-树上查找、插入和删除的读写盘的次数为O(logtn),CPU计算时间为O(mlogtn)。
2、性能分析
①n个结点的平衡的二叉排序的高度H(即lgn)比B-树的高度h约大lgt倍。
【例】若m=1024,则lgt=lg512=9。此时若B-树高度为4,则平衡的二叉排序树的高度约为36。显然,若m越大,则B-树高度越小。
②若要作为内存中的查找表,B-树却不一定比平衡的二叉排序树好,尤其当m较大时更是如此。
因为查找等操作的CPU计算时间在B-树上是
O(mlogtn)=0(lgn·(m/lgt))
而m/lgt>1,所以m较大时O(mlogtn)比平衡的二叉排序树上相应操作的时间O(lgn)大得多。因此,仅在内存中使用的B-树必须取较小的m。(通常取最小值m=3,此时B-树中每个内部结点可以有2或3个孩子,这种3阶的B-树称为2-3树)。